Rangkuman Momentum sudut partikel
Momentum Sudut partikel
Gambar 6.6 melukiskan sebuah titik partikel yang bermassa m sedang melakukan gerak rotasi
dengan jari-jari lintasan R dan dengan kecepatan v. Arah kecepatan sebuah titik partikel yang
melakukan gerak rotasi pada suatu titik merupakan arah garis singgung di titik tersebut.
Selama titik partikel melakukan gerak rotasi, karena mempunyai massa dan kecepatan maka titik partikel tersebut mempunyai momentum.
Momentum yang dimiliki oleh titik partikel yang melakukan gerak rotasi disebut dengan momentum sudut (momentum anguler), yang diberi lambang dengan L. Besar dari momentum sudut dinyatakan dengan persamaan:
m = massa (kg)
v = kecepatan (m/s)
R = jari-jari lintasan (m)
L = momentum sudut (kg m^2/s)
Dari persamaan L = m . v . R didapat m . v = p (momentum linier) sehingga didapat:

R = vektor posisi partikel
Arah momentum sudut dapat dicari dengan aturan tangan kanan yaitu ketika kita mengepalkan keempat jari kita dari arah R ke arah P maka arah ibu jari menunjukkan arah momentum sudut L. Lihat gambar 6.7 di bawah ini:
MOMENTUM SUDUT BENDA TEGAR
Momentum Sudut dari Benda Tegar Berotasi
Analisis Model: Sistem Terisolasi (Momentum Sudut)
Pernyataan ini sering dinamakan prinsip kekekalan momentum sudut dan merupakan dasar dari versi momentum sudut dari model sistem yang terisolasi. Prinsip ini mengikuti langsung dari Persamaan 11.13, yang menunjukkan bahwa jika
dari momentum sudut sistem adalah L = Iw(Persamaan 11.14), konservasi momentum sudut mensyaratkan bahwa produk I dan wharus tetap konstan. Oleh karena itu, perubahan dalam I untuk sistem yang terisolasi membutuhkan perubahan dalam w. Dalam hal ini,
kita dapat mengekspresikan prinsip kekekalan momentum sudut sebagai:
pi = pf (jika gaya eksternal total pada sistem adalah nol)
Li = Lf (jika torsi eksternal total pada sistem adalah nol)
Suatu sistem dapat diisolasi dalam hal satu bentuk ini tetapi tidak dalam hal lain. Jika sistem ini nonisolasi dalam hal momentum atau momentum sudut, itu sering akan nonisolated juga dalam hal energi karena sistem memiliki gaya total atau torsi di atasnya dan gaya total atau torsi akan melakukan usaha pada sistem. Kita bisa, bagaimanapun, mengidentifikasi sistem yang nonisolated dalam hal energi tapi sistem terisolasi dari segi momentum. Sebagai contoh, bayangkan untuk mendorong pada sebuah balon (sistem) antara tangan Anda. Gaya ini dilakukan untuk meniup balon, sehingga sistem ini nonisolated dalam hal energi, tapi ada nol gaya total pada sistem, sehingga sistem ini terisolasi dari segi momentum. Sebuah pernyataan yang sama dapat dibuat tentang memutar ujung panjang, sepotong logam kenyal dengan kedua tangan. Usaha ini dilakukan pada logam (sistem), sehingga energi yang tersimpan dalam sistem nonisolated sebagai energi potensial elastis, tetapi torsi total pada sistem adalah nol. Oleh karena itu, sistem ini terisolasi dari segi momentum sudut. Contoh lain adalah tumbukan benda makroskopik, yang merupakan sistem yang terisolasi dalam hal momentum, tetapi sistem nonisolated dalam hal energi karena output energi dari sistem dengan gelombang mekanik (suara) (Serway, 2010:326-330).
Contoh Soal Momentum Sudut
1. Suatu benda mempunyai momen inersia 2 kg m2 dan berotasi pada sumbu tetap dengan kecepatan sudut 1 rad/s. Berapa momentum sudut benda tersebut ?
Pembahasan
Diketahui :
Momen inersia (I) = 2 kg m2
Kecepatan sudut (ω) = 1 rad/s
Ditanya : Momentum sudut (L)
Jawab :
Rumus momentum sudut :
L = I ω
Keterangan : L = momentum sudut (kg m2/s), I = momen inersia (kg m2), ω = kecepatan sudut (rad/s)
Momentum sudut :
L = I ω = (2)(1) = 2 kg m2/s
2. Katrol cakram pejal bermassa 2 kg dan berjari-jari 0,1 meter. Jika katrol bergerak rotasi pada porosnya dengan kecepatan sudut konstan 2 rad/sekon, berapa momentum sudut katrol ?
Pembahasan
Diketahui :
Massa katrol cakram pejal (m) = 2 kilogram
Jari-jari katrol cakram pejal (r) = 0, 1 meter
Kecepatan sudut (ω) = 2 radian/sekon
Ditanya : Momentum sudut katrol
Jawab :
Rumus momen inersia cakram pejal jika berotasi pada poros seperti pada gambar :
I = 1/2 m r2
Keterangan : I = momen inersia (kg m2), m = massa (kg), r = jari-jari (meter)
Momen inersia cakram pejal :
I = 1/2 (2)(0,1)2 = (1)(0,01) = 0,01 kg m2
Momentum sudut :
L = I ω = (0,01)(2) = 0,02 kg m2/s
3. Bola pejal bermassa 2 kg dan berjari-jari 0,2 meter berotasi terhadap porosnya dengan kecepatan sudut 4 rad/s. Tentukan momentum sudut bola pejal!
Pembahasan
Diketahui :
Massa bola pejal (m) = 2 kilogram
Jari-jari bola pejal (r) = 0,2 meter
Kecepatan sudut (ω) = 4 radian/sekon
Ditanya : Momentum sudut bola pejal
Jawab :
Rumus momen inersia bola pejal jika berotasi pada poros seperti pada gambar :
I = (2/5) m r2
Keterangan : I = momen inersia (kg m2), m = massa (kg), r = jari-jari (meter)
Momen inersia bola pejal :
I = (2/5)(2)(0,2)2 = (4/5)(0,04) = 0,032 kg m2
Momentum sudut bola pejal :
L = I ω = (0,032)(4) = 0,128 kg m2/s
4. Benda bermassa 1 kg bergerak melingkar dengan kecepatan sudut tetap 2 rad/s. Tentukan momentum sudut jika jari-jari lintasan partikel 10 cm.
Pembahasan
Diketahui :
Massa benda (m) = 1 kilogram
Jari-jari bola pejal (r) = 10 cm = 10/100 = 0,1 meter
Kecepatan sudut (ω) = 2 radian/sekon
Ditanya : Momentum sudut
Jawab :
Rumus momen inersia partikel :
I = m r2 = (1)(0,1)2 = (1)(0,01) = 0,01 kg m2
Momentum sudut :
L = I ω = (0,01)(2) = 0,02 kg m2/s
5. Sebuah piringan berbentuk silinder pejal homogen mula-mula berputar pada porosnya dengan kelajuan sudut 5 rad/s. Bidang piringan sejajar bidang horizontal. Massa dan jari-jari piringan 2 kg dan 0,2 meter. Bila di atas piringan diletakkan cincin yang mempunyai massa 0,1 kg dan jari-jari 0,2 meter, di mana pusat cincin tepat di atas pusat piring, maka piringan dan cincin akan bersama-sama berputar dengan kecepatan sudut…
Pembahasan
Diketahui :
Massa silinder pejal (m1) = 2 kilogram
Jari-jari silinder pejal (r1) = 0,2 meter
Kelajuan sudut silinder pejal (ω1) = 5 rad/s
Massa cincin (m2) = 0,1 kilogram
Jari-jari cincin (r2) = 0,2 meter
Ditanya : Kelajuan sudut silinder dan cincin
Jawab :
Momen inersia silinder pejal : I = 1⁄2 m1r12 = 1⁄2 (2)(0,2)2 = (1)(0,04) = 0,04 kg m2
Momen inersia cincin : I = m r2 = (0,1)(0,2)2 = (0,1)(0,04) = 0,004 kg m2
Momen inersia silinder pejal dan cincin (I) = 0,04 + 0,004 = 0,044 kg m2
Momentum sudut awal (L1) = Momentum sudut akhir (L2)
I1 ω1 = I2 ω2
(0,04)(5) = (0,044)(ω2)
(0,2) = (0,044)(ω2)
ω2 = 0,2 : 0,044
ω2 = 4,5 rad/s
6. Seorang penari balet berputar dengan tangan terentang sepanjang 150 cm dan kecepatan sudut 10 radian/sekon. Lalu penari melipat tangannya menjadi 75 cm sepanjang siku. Berapa kecepatan sudut akhir ?
Pembahasan
Diketahui :
Jari-jari 1 (r1) = 150 cm = 1,5 meter
Jari-jari 2 (r2) = 75 cm = 0,75 meter
Kecepatan sudut 1 (ω1) = 10 rad/s
Ditanya : Kecepatan sudut 2 (ω2)
Jawab :
Momen inersia awal : I1 = m r12 = (m)(1,5)2 = 2,25 m
Momen inersia akhir : I2 = m r22 = (m)(0,75)2 = 0,5625 m
Momentum sudut awal (L1) = Momentum sudut akhir (L2)
I1 ω1 = I2 ω2
(2,25 m)(10) = (0,5625 m)(ω2)
22,5 m = (0,5625 m)(ω2)
22,5 = (0,5625)(ω2)
ω2 = 22,5 / 0,5625
ω2 = 40 rad/s

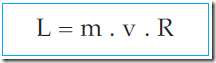







Comments
Post a Comment